El sistema d'Hondt es un método de promedio mayor para asignar escaños en sistemas de representación proporcional por listas electorales. Los métodos de promedio mayor se caracterizan por dividir a través de distintos divisores los totales de los votos obtenidos por los distintos partidos, produciéndose secuencias de cocientes decrecientes para cada partido y asignándose los escaños a los promedios más altos.1 2 Fue creado por el jurista belga Victor d'Hondt en 1878.3 4
 Los sistemas de representación proporcional intentan asignar los escaños a las listas de manera proporcional al número de votos recibidos. En general, no es posible alcanzar la proporcionalidad exacta, ya que no es posible asignar un número decimal de escaños. De los métodos comúnmente utilizados para la conversión proporcional de votos en escaños, el método d’Hondt, siendo bastante proporcional, tiende a favorecer un poco más que otros a los grandes partidos.5 6Sin embargo, hay dos circunstancias que favorecen muchísimo más a dichos partidos: las circunscripciones pequeñas y la barrera electoral.7
Los sistemas de representación proporcional intentan asignar los escaños a las listas de manera proporcional al número de votos recibidos. En general, no es posible alcanzar la proporcionalidad exacta, ya que no es posible asignar un número decimal de escaños. De los métodos comúnmente utilizados para la conversión proporcional de votos en escaños, el método d’Hondt, siendo bastante proporcional, tiende a favorecer un poco más que otros a los grandes partidos.5 6Sin embargo, hay dos circunstancias que favorecen muchísimo más a dichos partidos: las circunscripciones pequeñas y la barrera electoral.7
Al menos estos países utilizan el método d’Hondt para el reparto de votos en escaños: Albania, Argentina,8 Austria,9 Bélgica,9 Brasil, Bulgaria, Camboya, Cabo Verde, Chile,10 Colombia, República Dominicana,8 Croacia, República Checa, Timor del Este, Ecuador, España,11 9 Estonia, Finlandia,9 Guatemala,8 Hungría,Islandia,9 Israel, Japón, Kosovo, Luxemburgo, Macedonia, Moldovia, Montenegro, Países Bajos,9 Paraguay,8 Perú,8 Polonia, Portugal,9 Rumanía, Escocia, Serbia, Eslovenia, Turquía, Uruguay,8 y Gales.
Tras escrutar todos los votos, se calculan cocientes sucesivos para cada lista electoral. La fórmula de los cocientes es12
donde:
- V representa el número total de votos recibidos por la lista, y
- s representa el número de escaños que cada lista se ha llevado de momento, inicialmente 0 para cada lista.
El número de votos recibidos por cada lista se divide sucesivamente por cada uno de los divisores, desde 1 hasta el número total de escaños a repartir. La asignación de escaños se hace ordenando los cocientes de mayor a menor y asignando a cada uno un escaño hasta que estos se agoten. A diferencia de otros sistemas, el número total de votos no interviene en el cómputo.
Ejemplo 1[editar]
Supongamos unas elecciones a las que se presentan cinco partidos, entre los que deben repartirse siete escaños (o curules o bancas, según el país). Como el número total de votos no cuenta, el resultado sería el mismo si concurrieran más partidos con menos de 15.000 votos.
| Partido A | Partido B | Partido C | Partido D | Partido E | |
|---|---|---|---|---|---|
| Votos | 340 000 | 280 000 | 160 000 | 60 000 | 15 000 |
Antes de empezar la asignación de escaños se dibuja una tabla de 7 filas (número de escaños) por 5 columnas (número de partidos). En la primera fila se escribe el número total de votos recibidos por cada partido (divisor 1). Es preferible ordenar los partidos por número de votos, así se simplificarán las siguientes fases del algoritmo.
En cada iteración se calculan los cocientes para cada partido y se asigna un escaño al partido con el cociente mayor. Para la siguiente iteración se recalcula el cociente del partido que acaba de recibir un escaño. Los demás partidos mantienen su cociente, ya que no recibieron escaño, y se repite el proceso.
En la siguiente tabla se muestra el resultado de las siete iteraciones.
| Partido A | Partido B | Partido C | Partido D | Partido E | |
|---|---|---|---|---|---|
| Votos | 340 000 | 280 000 | 160 000 | 60 000 | 15 000 |
| Escaño 1 | (340 000/1 =) 340 000 | (280 000/1 =) 280 000 | (160 000/1 =) 160 000 | (60 000/1 =) 60 000 | (15 000/1 =) 15 000 |
| Escaño 2 | (340 000/2 =) 170 000 | (280 000/1 =) 280 000 | (160 000/1 =) 160 000 | (60 000/1 =) 60 000 | (15 000/1 =) 15 000 |
| Escaño 3 | (340 000/2 =) 170 000 | (280 000/2 =) 140 000 | (160 000/1 =) 160 000 | (60 000/1 =) 60 000 | (15 000/1 =) 15 000 |
| Escaño 4 | (340 000/3 =) 113 333 | (280 000/2 =) 140 000 | (160 000/1 =) 160 000 | (60 000/1 =) 60 000 | (15 000/1 =) 15 000 |
| Escaño 5 | (340 000/3 =) 113 333 | (280 000/2 =) 140 000 | (160 000/2 =) 80 000 | (60 000/1 =) 60 000 | (15 000/1 =) 15 000 |
| Escaño 6 | (340 000/3 =) 113 333 | (280 000/3 =) 93 333 | (160 000/2 =) 80 000 | (60 000/1 =) 60 000 | (15 000/1 =) 15 000 |
| Escaño 7 | (340 000/4 =) 85 000 | (280 000/3 =) 93 333 | (160 000/2 =) 80 000 | (60 000/1 =) 60 000 | (15 000/1 =) 15 000 |
| Escaños asignados | 3 | 3 | 1 | 0 | 0 |
| Escaños proporcionales | 2,78 | 2,29 | 1,31 | 0,49 | 0,12 |
En la siguiente tabla se muestra el mismo procedimiento, pero, en lugar de calcular los cocientes conforme se van asignando los escaños, se han calculado todos los cocientes en primer lugar. Cada fila corresponde a uno de los partidos y cada columna corresponde a un divisor. El número entre corchetes indica el número de orden en la secuencia. Las celdas verdes son aquellas a las que se ha asignado un escaño.
| /1 | /2 | /3 | /4 | /5 | /6 | /7 | Escaños asignados | Escaños proporcionales | |
|---|---|---|---|---|---|---|---|---|---|
| Partido A | [1] 340 000 | [3] 170 000 | [6] 113 333 | 85 000 | 68 000 | 56 667 | 48 571 | 3 | 2,78 |
| Partido B | [2] 280 000 | [5] 140 000 | [7] 93 333 | 70 000 | 56 000 | 46 667 | 40 000 | 3 | 2,29 |
| Partido C | [4] 160 000 | 80 000 | 53 333 | 40 000 | 32 000 | 26 667 | 22 857 | 1 | 1,31 |
| Partido D | 60 000 | 30 000 | 20 000 | 15 000 | 12 000 | 10 000 | 8571 | 0 | 0,49 |
| Partido E | 15 000 | 7500 | 5000 | 3750 | 3000 | 2500 | 2143 | 0 | 0,12 |
Ejemplo 2[editar]
En este ejemplo se usan los mismos datos ficticios que los usados en los ejemplos del método del resto mayor para permitir comparaciones. Suponiendo que se presenten siete partidos para elegir 21 escaños, los partidos reciben 1 000 000 de votos repartidos así:
| Partido A | Partido B | Partido C | Partido D | Partido E | Partido F | Partido G | |
|---|---|---|---|---|---|---|---|
| Votos | 391 000 | 311 000 | 184 000 | 73 000 | 27 000 | 12 000 | 2000 |
En la siguiente tabla se muestra el reparto. Cada fila corresponde a uno de los partidos y cada columna corresponde a un divisor. El número entre corchetes indica el número de orden en la secuencia. Las celdas verdes son aquellas a las que se ha asignado un escaño.
| /1 | /2 | /3 | /4 | /5 | /6 | /7 | /8 | /9 | /10 | Escaños asignados | Escaños proporcionales | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Partido A | [1] 391 000 | [3] 195 500 | [6] 130 333 | [8] 97 750 | [10] 78 200 | [13] 65 166 | [16] 55 857 | [18] 48 875 | [21] 43 444 | 39 100 | 9 | 8,21 |
| Partido B | [2] 311 000 | [5] 155 500 | [7] 103 666 | [11] 77 750 | [14] 62 200 | [17] 51 833 | [20] 44 428 | 38 875 | 34 555 | 31 100 | 7 | 6,53 |
| Partido C | [4] 184 000 | [9] 92 000 | [15] 61 333 | [19] 46 000 | 36 800 | 30 666 | 26 285 | 23 000 | 20 444 | 18 400 | 4 | 3,86 |
| Partido D | [12] 73 000 | 36 500 | 24 333 | 18 250 | 14 600 | 12 166 | 10 428 | 9125 | 8111 | 7300 | 1 | 1,53 |
| Partido E | 27 000 | 13 500 | 9000 | 6750 | 5400 | 4500 | 3857 | 3375 | 3000 | 2700 | 0 | 0,57 |
| Partido F | 12 000 | 6000 | 4000 | 3000 | 2400 | 2000 | 1714 | 1500 | 1333 | 1200 | 0 | 0,25 |
| Partido G | 2000 | 1000 | 666 | 500 | 400 | 333 | 285 | 250 | 222 | 200 | 0 | 0,04 |



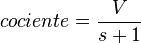








No hay comentarios:
Publicar un comentario